We explore solutions to a Martin Gardner puzzel using math and then modeling it with CAD software with no real intention to 3d print our solutions.

From My Best Mathematical and Logic Puzzles. dover ![]()
analysis
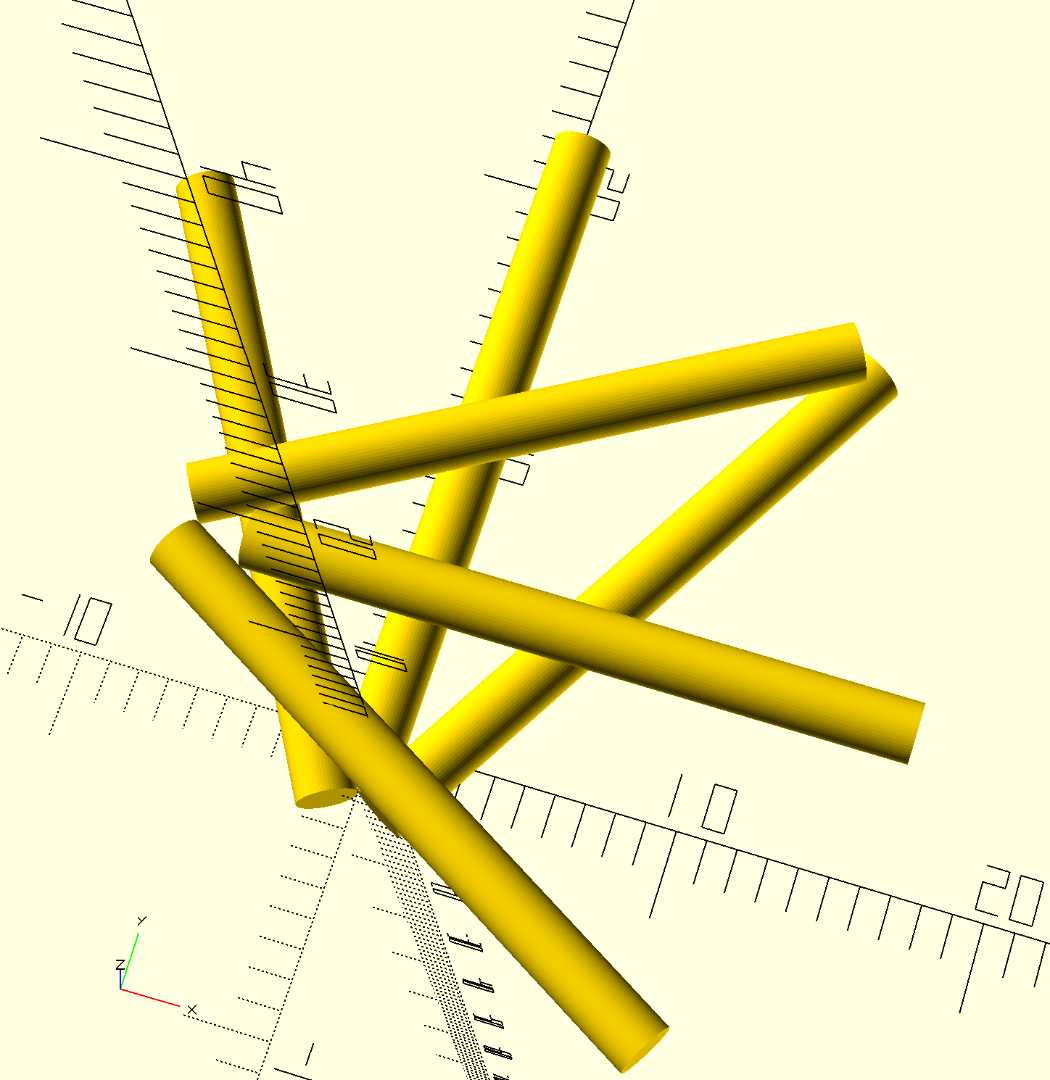
The problem: Six cylinders (pencils or cigarettes) arranged so that each one touches all five of the others.
I will describe this in the same manner as you were doing with your cad program.
Start with a cylinder of radius R, length L. The center of the base of the cylinder is at the origin. I’ll take the horizontal axis as x and the vertical as y, with z coming out of the screen toward the viewer.
Assume: L increases in the +y direction.
module pencil() { rotate([-90,0,0]) cylinder(h=L,r=R); }
# 1. Triangle 1
Make a copy of the cylinder.
Rotate that cylinder to the right by angle w.
Translate the cylinder: In the x direction by R * cos w. In the y direction by - R * (sin w + 1/tan w).
translate([R*cos(w), -R*(sin(w)+1/tan(w)), 0]) rotate([0,0,-w]) pencil();
This translates it down and to the right.
Copy the original cylinder. Rotate this one by an angle -w. Translate it as before but reverse the x direction to -R * cos w. This translates it down and to the left.
translate([-R*cos(w), -R*(sin(w)+1/tan(w)), 0]) rotate([0,0,-(-w)]) pencil();
The three cylinders form one “triangle” of the sort you wrote before. Each cylinder touches the other two.
For the specific “equilateral” case where the rotation is by w = 30 degrees, the angled cylinders have the origin of their base at X = +/- 0.866 * R Y = 0.5 * R (Using sin w = 1/2, cos w = sqrt(3)/2.)
# 2. Triangle 2.
Make a copy of Triangle 1. Shift it in the z direction by 2*R so the new triangle sits atop the first triangle.
Now one has to make choices about how one wants the result to look. The most symmetric choice is the following:
Rotate the second triangle by 90 degrees clockwise about the origin. So the base of the middle cylinder is still centered on the origin.
Translate the second triangle up and to the left by an amount D each way. So Translate in x direction by -D. Translate in y direction by D.
The choice of D determines whether all the cylinders touch or not, and how much of an overlap there is. Let’s denote by f the point where the two most separated cylinders touch. This is expressed as a fraction of the cylinder length. So to touch, we need 0 < f < 1.
If f = 1, the two farthest cylinders just touch at their farther tips. If f > 1, the cylinders won’t touch.
This fraction f depends on the cylinder dimensions R and L, and the choice of translation point D (used above).
The formula for f is
f = a * D/L + b * R/L
Where a and b depend on the rotation angle w. For the case of w = 30 degrees,
a = 2.7322
b = 4.7324
In general,
a = 1/(cos w - sin w)
b = a/(tan w)
By choosing a pleasing value for f, for example, f = 0.78, one finds the relation between cylinder length, radius and crossing point (D) that enables all six cylinders to touch each of the other.
Choosing f, R, L, and D also places a restriction on the point of touch of the two cylinders closest to each other.
a = 1/(cos(w) - sin(w)); b = a/(tan(w)); f = 0.8; D = (f - b * R/L)*L/a; triangle(); translate([-D,D,2*R]) rotate([0,0,-90]) triangle();
For the 30 degree case, this touching point is at 0.27 * f of the length of a cylinder. (Choosing f=0.78 makes this nearest touching point have the same overlap as the farthest touching point in this case.)
implementation
We're very close but can't find a way to close the final gap without opening another gap.
pages/touching-cylinders
See OpenSCAD
Uploaded image